Recursive subquery factoring (aka recursive common table expressions) is a feature first introduced in Oracle version 11gR2 that has been used by many both for business and for play. See for example this post on Jonathan Lewis blog, this post on solving sudokus and this about the Mandelbrot set. The computational strength of the feature comes from the fact that it makes recursion easily available from within SQL and so opens the door to natural ways of implementing several algorithms for numerical computation.
Additional note: the amount of physics and maths used have been kept to a minimum and simplified where possible, hopefully without introducing too many mistakes in the process.
Example 1: projectile in gravity field
The motion is on 1 dimension, say the x axis. Our first task is to find a representation of the state of the system with a structure that can be computed in the database. A natural choice is to use the tuple (t, x, v, a). Where t is time, x is the position along the 1-dimensional axis of motion, v is the velocity and a is the acceleration.
Newton's second law (F=ma) gives us the rule of the game when we want to compute the state of the system subject to and external force. Using calculus this can be written as:

Next we need a method to find numerical (approximate) solutions. We can use the Euler integration method, which basically means doing the following:
Another important point is that we need to know the initial conditions for the state tuple, in particular initial position and velocity. In the example we will take x(t=0)=0 m and v(t=0)=100 m/sec. The force is the gravitational pull at the surface of the Earth: F=--m*g, where g=9.81 m/sec^2. Note the mass cancels out in our equations. This example models the motion of a projectile that we shoot vertically into the air and we observe as it rises up to about 500 meters and then falls back down, all this happens in about 20.5 seconds. The SQL used and a graph of the results are here below:
define dT=0.1
define g=9.81
define maxT=20
-- SQL to compute the motion of a projectile subject to gravity
WITH data(t,x,v,a) AS (
SELECT cast(0 as binary_double) t, cast(0 as binary_double) x, cast (100 as binary_double) v, cast(-&g as binary_double) a FROM dual
UNION ALL
SELECT t+&dT, x+v*&dT, v+a*&dT, -&g FROM data WHERE t < &maxT
)
SELECT t,x,v,a FROM data;
Example 2: Harmonic oscillator
In this example we investigate the motion of a mass attached to a spring. We expect the mass to oscillate around a central point (x=0).
For greater accuracy in calculations we use a different integration method: the Verlet integration method (see also this link). The equation for the acceleration is: a = F/m =-K*x and initial conditions are: x(t=0)=1 m and v(t=0)=0 m/sec. Moreover we take K= 0.1 sec^-2. See below the SQL used for the calculation and a graph of the results.
define dT=0.1
define K=0.1
define maxT=20
-- SQL to compute the motion of a harmonic oscillator
WITH data(t,x,v,a) AS (
SELECT cast(0 as binary_double) t, cast(1 as binary_double) x, cast (0 as binary_double) v, cast(-&K*1 as binary_double) a FROM dual
UNION ALL
SELECT t+&dT, x+v*&dT+0.5*a*&dT*&dT, v+0.5*(a-&K*(x+v*&dT))*&dT, -&K*(x+v*&dT+0.5*a*&dT*&dT) FROM data WHERE t < &maxT
)
SELECT t,x,v,a FROM data;
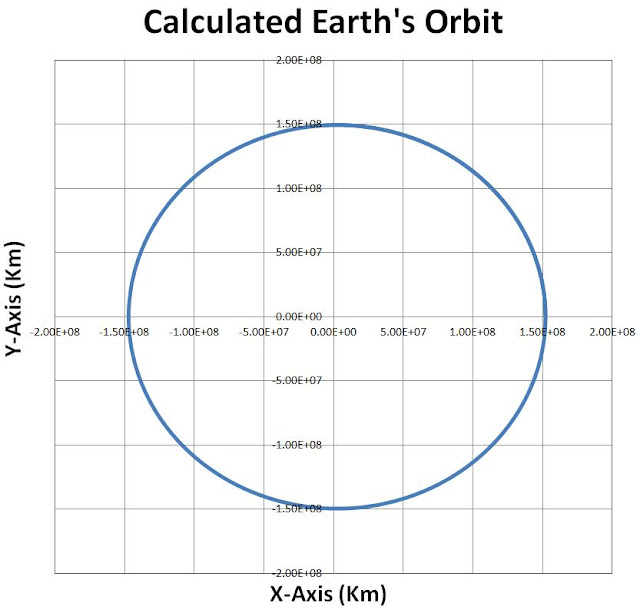
The motion of the system Earth-Sun is a problem of 2 bodies moving in space. With a 'standard trick' this can be reduced to a problem of 1 body, and 2 spatial variables, which represent the (vector) distance of the Earth from the Sun in the place of the orbit. Our description of the system will use the following tuple: (t,x,vx,ax,y,vy,ay), that is time, position, velocity and acceleration for a 2-dimensional problem in the (x,y) plane. The equation for the force is Newton's law of universal gravitation. Another important point again is to use the correct initial conditions. These can be taken from astronomical observations, x(t=0)=152098233 Km (also know as the aphelion point) and v=29.291 Km/sec (credits to this link and this other link). We will use again the Verlet integration method as in example 2 above. Note, for ease of computation, time and space will be re-scaled so that t=1 means 1000 sec and x=1 means 1 Km (same is true for the y axis). The SQL used is pasted here below as well as a graph of the computed results, that is our approximate calculation of the Earth's orbit.
-- length unit = 1 km
-- time unit = 1000 sec
define dT=.1
define aph=152098233
define GM=132712838618000000
-- note this is GM Sun + Earth (reduced mass correction)
define v_aph=29291
define maxT=40000
-- SQL to compute the trajectory of the Earth around the Sun
WITH data(step, t,x,y,vx,vy,ax,ay) AS (
SELECT 0 step,cast(0 as binary_double) t,cast(&aph as binary_double) x,cast(0 as binary_double) y,
cast(0 as binary_double) vx, cast(&v_aph as binary_double) vy,
cast(-&GM/power(&aph,2) as binary_double) ax, cast(0 as binary_double) ay FROM dual
UNION ALL
SELECT step+1, t+&dT, x+vx*&dT+0.5*ax*&dT*&dT, y+vy*&dT+0.5*ay*&dT*&dT,
vx+0.5*(ax-&GM*(x+vx*&dT)/power(x*x+y*y,1.5))*&dT,
vy+0.5*(ay-&GM*(y+vy*&dT)/power(x*x+y*y,1.5))*&dT,
-&GM*(x+vx*&dT+0.5*ax*&dT*&dT)/power(power(x+vx*&dT,2)+power(y+vy*&dT,2),1.5),
-&GM*(y+vy*&dT+0.5*ay*&dT*&dT)/power(power(x+vx*&dT,2)+power(y+vy*&dT,2),1.5)
FROM data WHERE t < &maxT
)
SELECT t,x,y,vx,vy,ax,ay FROM data WHERE mod(step,100)=0; -- output only one point every 100
Example 4: Compute the length of the sidereal year using the equations of motion of the Earth around the Sun and SQL
As a final example and an 'application' of the techniques above we can use SQL to compute the number of days year (or rather in a sidereal year, see the link for additional details). We find a result that is in agreement with measurements with 6 significant digits. This is an interesting result considering that it is obtained with just a few lines of SQL!
-- SQL to compute the number of days in one sidereal year
-- A sidereal year is the time taken by the Earth to orbit
-- the Sun once with respect to the fixed stars.
-- This builds on the equation and SQL discussed in example N.3
define dT=.1
define aph=152098233
define GM=132712838618000000
define v_aph=29291
define maxT=40000
select round(t*1000/(3600*24),3) days_in_a_sidereal_year from (
define aph=152098233
define GM=132712838618000000
define v_aph=29291
define maxT=40000
select round(t*1000/(3600*24),3) days_in_a_sidereal_year from (
WITH data(step, t,x,y,vx,vy,ax,ay) AS (
SELECT 0 step,cast(0 as binary_double) t,cast(&aph as binary_double) x,cast(0 as binary_double) y,
cast(0 as binary_double) vx, cast(&v_aph as binary_double) vy,
cast(-&GM/power(&aph,2) as binary_double) ax, cast(0 as binary_double) ay FROM dual
UNION ALL
SELECT step+1, t+&dT, x+vx*&dT+0.5*ax*&dT*&dT, y+vy*&dT+0.5*ay*&dT*&dT,
vx+0.5*(ax-&GM*(x+vx*&dT)/power(x*x+y*y,1.5))*&dT,
vy+0.5*(ay-&GM*(y+vy*&dT)/power(x*x+y*y,1.5))*&dT,
-&GM*(x+vx*&dT+0.5*ax*&dT*&dT)/power(power(x+vx*&dT,2)+power(y+vy*&dT,2),1.5),
-&GM*(y+vy*&dT+0.5*ay*&dT*&dT)/power(power(x+vx*&dT,2)+power(y+vy*&dT,2),1.5)
FROM data WHERE t < &maxT
)
SELECT step,t,y,lead(y) over(order by step) next_y FROM data
) where y<0 and next_y>0;
DAYS_IN_A_SIDEREAL_YEAR
-----------------------
365.256